Formules voor omtrek en oppervlakte

Omtrek is de afstand rond een vorm, terwijl oppervlakte het gebied is dat erin zit. Daniel Grizelj / Getty Images

Perimeter en oppervlakteformules zijn gebruikelijk geometrie berekeningen gebruikt in wiskunde en wetenschap. Hoewel het een goed idee is om deze formules uit het hoofd te leren, is hier een lijst met formules voor omtrek, omtrek en oppervlakte die u als handige referentie kunt gebruiken.

Belangrijkste aandachtspunten: omtrek- en oppervlakteformules

• De omtrek is de afstand rond de buitenkant van een vorm. In het speciale geval van de cirkel wordt de omtrek ook wel de omtrek genoemd.
• Hoewel calculus nodig kan zijn om de omtrek van onregelmatige vormen te vinden, is geometrie voldoende voor de meeste regelmatige vormen. De uitzondering is de ellips, maar de omtrek kan worden benaderd.
• Oppervlakte is een maat voor de ruimte die is ingesloten in een vorm.
• Omtrek wordt uitgedrukt in eenheden van afstand of lengte (bijv. mm, ft). De oppervlakte wordt gegeven in termen van vierkante afstandseenheden (bijv. cm^twee, voet^twee).

Driehoeksomtrek- en oppervlakteformules

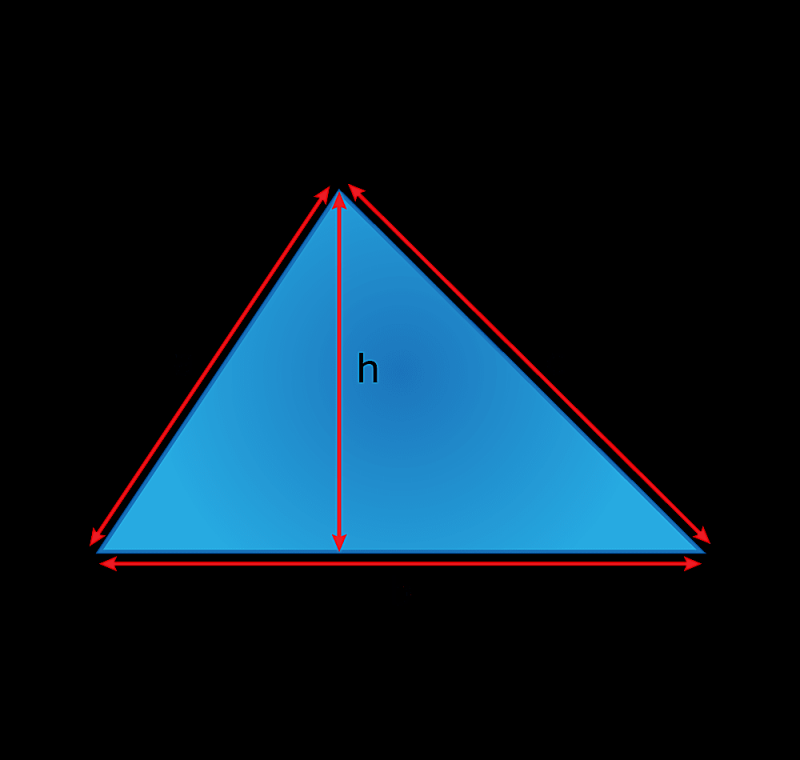
Een driehoek heeft drie zijden. Todd Helmenstine

EEN driehoek is een driezijdig gesloten figuur.
De loodrecht afstand van de basis tot het tegenoverliggende hoogste punt wordt de hoogte (h) genoemd.

Omtrek = a + b + c

Oppervlakte = ½bh

Vierkante omtrek- en oppervlakteformules

Vierkanten zijn vierzijdige figuren waarbij elke zijde even lang is. Todd Helmenstine

Een vierkant is een vierhoek waarbij alle vier zijden(en) even lang zijn.

Omtrek = 4s

Oppervlakte = s^twee

Formules voor rechthoekomtrek en oppervlaktegebied

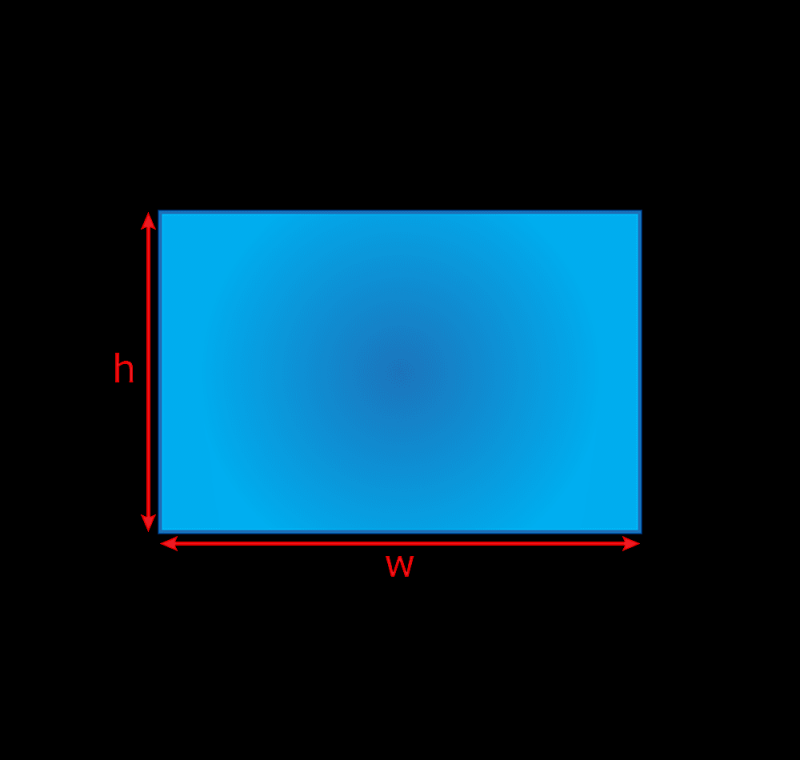
Een rechthoek is een vierzijdige figuur waarbij alle binnenhoeken rechte hoeken zijn en overstaande zijden even lang zijn. Todd Helmenstine

Een rechthoek is een speciaal soort vierhoek waar al het interieur hoeken zijn gelijk aan 90° en alle tegenoverliggende zijden zijn even lang. De omtrek (P) is de afstand rond de buitenkant van de rechthoek.

P = 2u + 2w

Oppervlakte = h x w

Formules van parallellogramomtrek en oppervlaktegebied

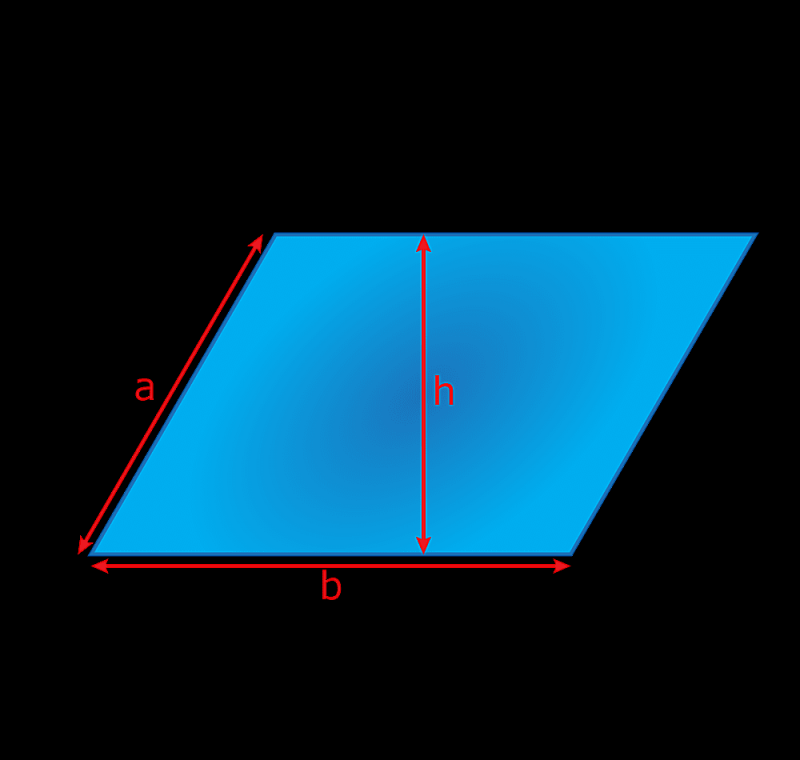
Een parallellogram is een vierhoek waarvan de overstaande zijden evenwijdig aan elkaar zijn. Todd Helmenstine

Een parallellogram is een vierhoek waarvan de overstaande zijden evenwijdig aan elkaar zijn.
De omtrek (P) is de afstand rond de buitenkant van het parallellogram.

P = 2a + 2b

De hoogte (h) is de loodrechte afstand van de ene evenwijdige zijde tot de tegenoverliggende zijde

Oppervlakte = b x h

Het is belangrijk om bij deze berekening de juiste zijde te meten. In de afbeelding wordt de hoogte gemeten van zijde b tot de tegenoverliggende zijde b, dus de oppervlakte wordt berekend als b x h, niet als a x h. Als de hoogte gemeten zou worden van a tot a, dan zou de oppervlakte a x h zijn. Conventie noemt de zijde waarvan de hoogte loodrecht staat op de 'baseren.' In formules wordt de basis meestal aangeduid met een b.

Trapeziumvormige omtrek- en oppervlakteformules

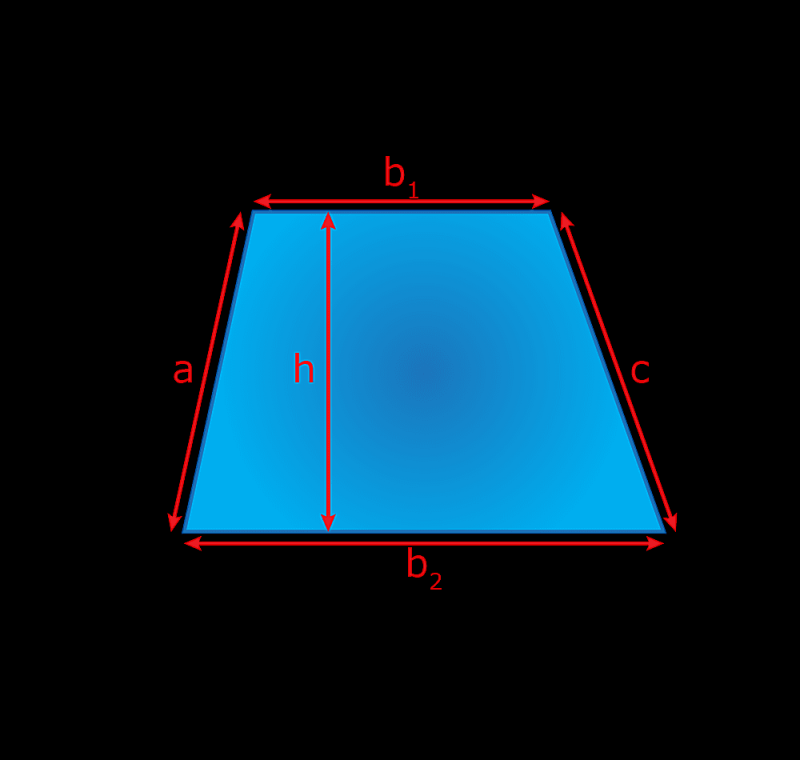
Een trapezium is een vierhoek waar slechts twee tegenover elkaar liggende zijden evenwijdig aan elkaar zijn. Todd Helmenstine

Een trapezium is een andere speciale vierhoek waar slechts twee zijden evenwijdig aan elkaar zijn. De loodrechte afstand tussen de twee evenwijdige zijden wordt de hoogte (h) genoemd.

Omtrek = a + b₁+ b_twee+ c

Oppervlakte = ½( b₁+ b_twee) x h

Formules cirkelomtrek en oppervlaktegebied

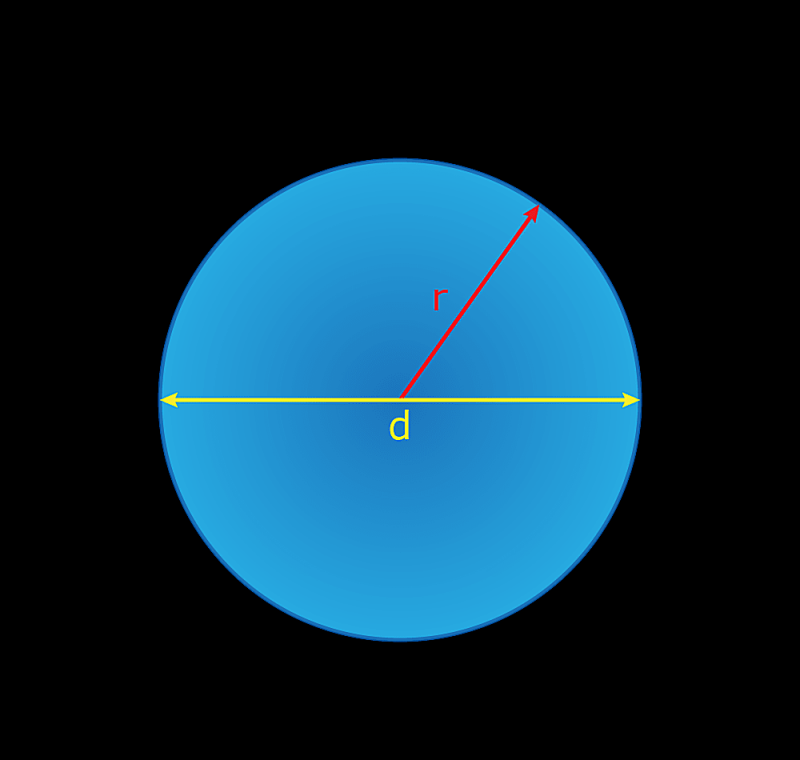
Een cirkel is een pad waarbij de afstand tot een middelpunt constant is. Todd Helmenstine

EEN cirkel is een ellips waarbij de afstand van het midden tot de rand constant is.
Omtrek (c) is de afstand rond de buitenkant van de cirkel (de omtrek).
Diameter (d) is de afstand van de lijn door het middelpunt van de cirkel van rand tot rand. Straal (r) is de afstand van het middelpunt van de cirkel tot de rand.
De verhouding tussen de omtrek en de diameter is gelijk aan het getal π.​

d = 2r

c = πd = 2πr

Oppervlakte = πr^twee

Formules van ellipsomtrek en oppervlaktegebied

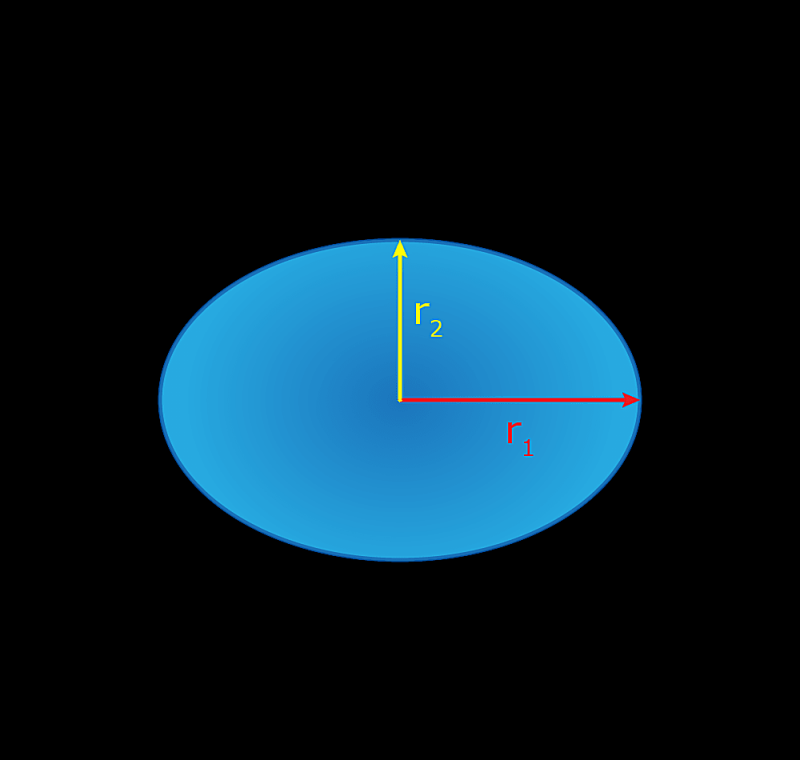
Een ellips is een figuur die wordt omlijnd door een pad waarbij de som van de afstanden van twee brandpunten constant is. Todd Helmenstine

Een ellips of ovaal is een figuur die wordt uitgetekend waarbij de som van de afstanden tussen twee vaste punten een constante is. De kortste afstand tussen het middelpunt van een ellips en de rand wordt de halve korte as genoemd (r₁) De langste afstand tussen het middelpunt van een ellips en de rand wordt de halve lange as genoemd (r_twee).

Het is eigenlijk best moeilijk om de omtrek van een ellips te berekenen! De exacte formule vereist een oneindige reeks, dus benaderingen worden gebruikt. Een algemene benadering, die kan worden gebruikt als r_tweeis minder dan drie keer groter dan r₁(of de ellips is niet te 'squished') is:

Omtrek ≈ 2π [ (a^twee+ b^twee) / twee ]

Oppervlakte = πr₁r_twee

Hexagon omtrek- en oppervlakteformules

Een regelmatige zeshoek is een zeshoekige veelhoek waarvan elke zijde even lang is. Todd Helmenstine

Een regelmatige zeshoek is een zeshoekige veelhoek waarvan elke zijde even lang is. Deze lengte is ook gelijk aan de straal (r) van de zeshoek.

Omtrek = 6r

Oppervlakte = (3√3/2 )r^twee

Octagon-omtrek- en oppervlakteformules

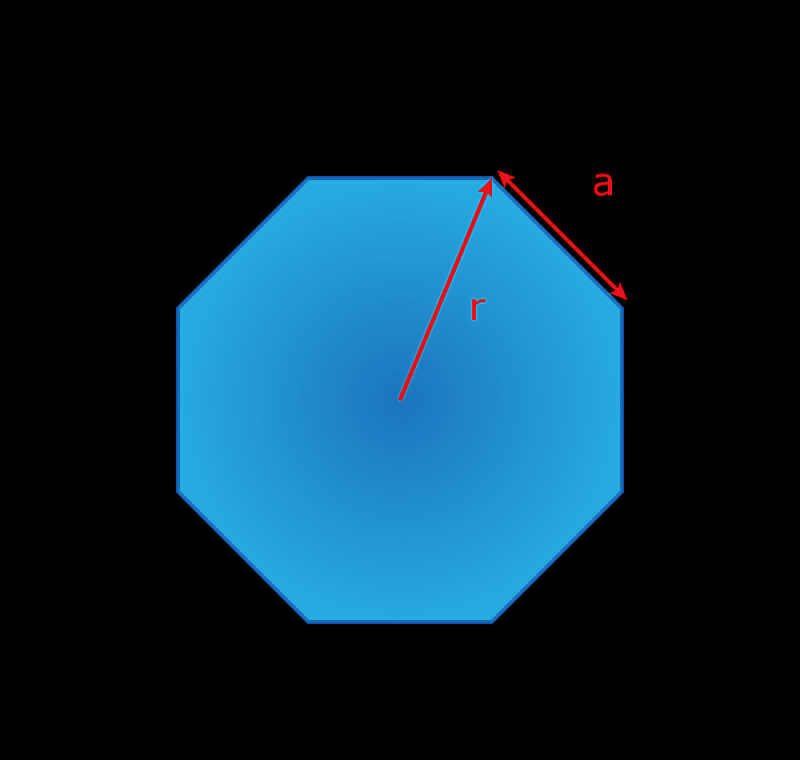
Een regelmatige achthoek is een achtzijdige veelhoek waarbij elke zijde even lang is. Todd Helmenstine

Een regelmatige achthoek is een achthoekige veelhoek waarvan elke zijde even lang is.

Omtrek = 8a

Oppervlakte = ( 2 + 2√2 )a^twee